Padmal's BLOG

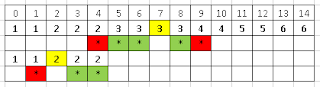
Lab3.2 The Skyline Problem The skyline problem is defined as given n rectangular buildings in a 2-dimensional city, compute the skyline of these buildings, eliminating hidden lines. The main task is to view buildings from a side and remove all sections that are not visible. All buildings share common bottom and every building can be represented by triplet (Left, Height, Right) As an example, if the buildings array is [ [1, 11, 5], [2, 6, 7], [3, 13, 9], [12, 7, 16], [14, 3, 25], [19, 18, 22], [23, 13, 29], [24, 4, 28] ] then the skyline is [[1, 11], [3, 13], [9, 0], [12, 7], [16, 3], [19, 18], [22, 3], [23, 13], [29, 0]] copyrights

Lab3.1 Finding the Odd Number of Occurrence You are given a sorted list of numbers where one number appears odd number of times. All other numbers appear even number of times. You are required to design an efficient algorithm to find the number that appears odd number of times. I'm using the Use Divide and Conquer method which runs at $\Theta(\log(n))$ As an example, if the sorted list is [1, 1, 2, 2, 2, 3, 3, 3, 3, 4, 4, 5, 5, 6, 6] then the odd occurrence number is 2