The Skyline Problem

Lab3.2 The Skyline Problem

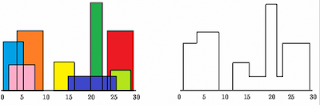
The skyline problem is defined as given n rectangular buildings in a 2-dimensional city, compute the skyline of these buildings, eliminating hidden lines. The main task is to view buildings from a side and remove all sections that are not visible. All buildings share common bottom and every building can be represented by triplet (Left, Height, Right)

As an example, if the buildings array is

     [
        [1, 11, 5],
        [2, 6, 7],
        [3, 13, 9],
        [12, 7, 16],
        [14, 3, 25],
        [19, 18, 22],
        [23, 13, 29],
        [24, 4, 28]
      ]

then the skyline is
[[1, 11], [3, 13], [9, 0], [12, 7], [16, 3], [19, 18], [22, 3], [23, 13], [29, 0]]

copyrights

buildings = [
                [1, 11, 5],
                [2, 6, 7],
                [3, 13, 9],
                [12, 7, 16],
                [14, 3, 25],
                [19, 18, 22],
                [23, 13, 29],
                [24, 4, 28]
            ]

def getSkyLine(B):
    return list(([B[0], B[1]], [B[2], 0]))

def setSkyLine(B1, B2):
    # B1 = Sky line of building 1 & B2 = Sky line of building 2
    h1 = 0; h2 = 0 # Height of buildings from B1 & B2
    # Skyline to return
    SkyLine = []
    # Indexes to iterate through each building set
    B1_i = 0; B2_i = 0;
    while ((len(B1) > B1_i) and (len(B2) > B2_i)):
        # Compare x position of each building
        if (B1[B1_i][0] <= B2[B2_i][0]):
            # h1 gets the first strip height
            h1 = B1[B1_i][1]
            # Add the current maximum height as the
            # height of the current strip
            if h1 >= h2: newHeight = h1
            else: newHeight = h2
            # Create the new strip of the skyline and
            # add it to the skylines building up
            if not ((len(SkyLine) != 0) and (SkyLine[len(SkyLine) - 1][1] == newHeight)):
                SkyLine.append([B1[B1_i][0], newHeight])
            # Increment the index to move to the next
            # building strip
            B1_i = B1_i + 1
        else:
            # h2 gets the first strip height
            h2 = B2[B2_i][1]
            # Add the current maximum height as the
            # height of the current strip
            if h1 >= h2: newHeight = h1
            else: newHeight = h2
            # Create the new strip of the skyline and
            # add it to the skylines building up
            if not ((len(SkyLine) != 0) and (SkyLine[len(SkyLine) - 1][1] == newHeight)):
                SkyLine.append([B2[B2_i][0], newHeight])
            # Increment the index to move to the next
            # building strip
            B2_i = B2_i + 1

    # If there are elements left in B1 or B2, that means
    # they are higher strips

    while (B1_i < len(B1)):
        # h1 gets the first strip height
        h1 = B1[B1_i][1]
        # Add the current maximum height as the
        # height of the current strip
        if h1 >= h2: newHeight = h1
        else: newHeight = h2
        # Add it to the skylines building up
        if not ((len(SkyLine) != 0) and (SkyLine[len(SkyLine) - 1][1] == newHeight)):
            SkyLine.append([B1[B1_i][0], newHeight])
        B1_i = B1_i + 1
        
    while (B2_i < len(B2)):
        # h2 gets the first strip height
        h2 = B2[B2_i][1]
        # Add the current maximum height as the
        # height of the current strip
        if h1 >= h2: newHeight = h1
        else: newHeight = h2
        # Add it to the skylines building up
        if not ((len(SkyLine) != 0) and (SkyLine[len(SkyLine) - 1][1] == newHeight)):
            SkyLine.append([B2[B2_i][0], newHeight])
        B2_i = B2_i + 1

    # Return the skyline calculated
    return SkyLine

def FindSkyLine(B):
    # Calculate length of B
    length = len(B)
    # If there's only one building,
    if (length == 1):
        return getSkyLine(B[0])
    else:
        # Find the mid point to break the set of buildings
        mid_value = length / 2
        # Find skyline of both set
        B1 = FindSkyLine(B[:mid_value]);
        B2 = FindSkyLine(B[mid_value:]);
        return setSkyLine(B1, B2)

print FindSkyLine(buildings)