Functions

Definition

Let A and B be two subsets of ℝ
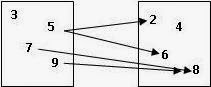
A relation from A to B is a rule which assigns a member of B to each member of A.

Definition

Let A and B are two subsets of ℝ
A function from A to B is a rule which assigns a unique member of B of each number of A.

In the example above, 5 being assigned to both 2 & 6. Hence the relation in that example is not a function.

Here is an example for a function;

Definition

Let f: A → B a function.

If f(x₁) = f(x₂) ⇒ x₁ = x₂
We say that f is an one to one function

In the previous example f_o(1) = f_o(9) but 1 ≠ 9
∴ f_o is not a one to one function.

Definition

Let f: A → B be a function

If ∀y ∈ B, ∃x ∈ A s.t. f(x) = y
We say that f is an onto function

In the previous example ∃!x s.t. f_o(x) = 4
∴ f_o is not an onto function

Definition

Let f: A → B be a function.

If f is both one to one and onto, we say that f is a bijection

In the previous example f_o is neither one to one nor onto.
∴ f_o is far from being bijection

Definition

Let f: A → B be a function

1. A is called the Domain of A
  We write D(f) = A

2. The following set is called the range of f
  R(f) = {y | y ∈ B & y = f(x) for some x ∈ A}

When B = R(f), f is an onto function

Definition

Let f: A → B be a function

1. If x₁ < x₂ ⇒ f(x₁) ≤ f(x₂), f is an increasing function
2. If x₁ < x₂ ⇒ f(x₁) < f(x₂), f is an strictly increasing function
3. If x₁ < x₂ ⇒ f(x₁) ≥ f(x₂), f is an decreasing
4. If x₁ < x₂ ⇒ f(x₁) > f(x₂), f is an strictly decreasing function

Eg: f: R → R
f(x) = 2x + 7

x₁ = x₂ ⇒ 2x₁ = 2x₂ ⇒ 2x₁ + 7 = 2x₂ + 7
⇒ f(x₁) = f(x₂)
∴ f is a function.

x₁ < x₂ ⇒ 2x₁ < 2x₂ ⇒ 2x₁ + 7 < 2x₂ + 7
∴ f is a strictly increasing function.

Definition

Let x ∈ R

The greatest integer less than or equal to x is denoted by [x]
Eg: [7.3] = 7

Definition

Let f: A → B be a function

The inverse relation f^-1 R(f) → A is defined in the following manner.
f^-1(y) = x where y = f(x) for some x ∈ A

in general f^-1 is not a function

Theorem

Let f: A → B be a function.
Then f^-1 is a function ⇔ f is one to one

Proof

Assume f^-1 is a function. Let f(x₁) = f(x₂)

Write f(x₁) = f(x₂) = y

f(x₁) = y ⇒ f^-1(y) = x₁
f(x₂) = y ⇒ f^-1(y) = x₂
x₁ = x₂ because f^-1 is a function
∴ f is one to one.

Assume f is one to one
Let y ∈ R(f) suppose f^-1(y) = x₁ & f^-1(y) = x₂
f^-1(y) = x₁ ⇒ f(x₁) = y
f^-1(y) = x₂ ⇒ f(x₂) = y
f(x₁) = f(x₂) & f is one to one
∴ x₁ = x₂

∴ f^-1 is a function

Definition

Let f: A → B & g: A → B be two functions

1. f + g: A → B
  (f + g)(x) = f(x) + g(x)

2. f - g: A → B
  (f - g)(x) = f(x) - g(x)

3. rf: A → B
  (rf)(x) = rf(x)

4. fg: A → B
  (fg)(x) = f(x).g(x)

5. f/g: A → B
  (^f/_g)(x) = ^f(x)/_g(x)  (g(x) ≠ 0)

Composition

Definition

Let f: A → B & g: B → C be two functions. The composite function (g _o f) is defined as
g _o f: A → C
(g _o f)(x) = g(f(x))

eg:

f: R → R	g: R[-1, 1]
f(x) = x2 – 3x + 2	g(x) = sin x

g _o f: R → [-1, 1]
(g _o f)(x) = g(f(x)) = g(x₂ – 3x + 2) = sin(x₂ – 3x + 2)

A function f: R → R is said to be an additive function if the following condition satisfied.

f(x + y) = f(x) + f(y) ∀x, y ∈ ℝ


Prove the following fact for an additive function.

1. f(0) = 0
2. f(rx) = rf(x) ∀r ∈ ℚ, ∀x ∈ ℝ

Proof of i.

0 + 0 = 0 ⇒ f(0 + 0) = f(0)
f(0) + f(0) = f(0) because f is additive.

∴ f(0) = 0

Proof of ii.

Let m ∈ ℤ⁺

Claim: f(mx) = mf(x) ∀x ∈ ℝ
It is clearly true for m = 1

Assume the claim is true for m = k
f{(k + 1)x} = f(kx + x) = f(kx) + f(x) [because f is additive]

= kf(x) + f(x)
=(k + 1)f(x)

∴ The claim is true for m = k + 1
∴ By induction, claim is true ∀m ∈ ℤ⁺


Let m ∈ ℤ^-

Now m + n = 0 ⇒ (m + n)x = 0.x = 0

∴ f(mx + nx) = f(0) = 0 [by part I]
∴ f(mx) + f(nx) = 0 [because f is additive]

f(mx) + f(nx) = 0
f(mx) = -nf(x) = mf(x)

So we have proved that f(mx) = mf(x) ∀m ∈ ℤ

Let r ∈ ℚ
Write r = ^m/_n with m ∈ ℤ, n ∈ ℤ⁺
Let x ∈ ℝ    x = n(¹/_nx)

f(x) = f[n(¹/_nx)] = nf(¹/_nx)
¹/_nf(x) = f(¹/_nx)
f(rx) = f(^m/_nx) = f[m(¹/_nx)] = mf(¹/_nx)
= m.¹/_nf(x) = ^m/_nf(x) = rf(x)